工程管理の統計学　-バラツキ具合を上手に評価する手法とは

偏差（バラツキ）を算出してできることとは？

生産工程の４M管理（原料、設備、人、工程や確認方法）において、
「バラツキ具合」「出来高」「信頼性」「安定性」「連続性」「効率」「精度」「良品率」「歩留まり」･･･Ａ
などの現状評価を行い際にデータを集めて標準偏差を出したりしますよね。
標準偏差というのは、平均値からの散らばり具合がどれくらいのおおきさになるのか、数値であらわしたものです。
この散らばり具合を見ることで、Ａの評価を理論的に行うことが出来ます。
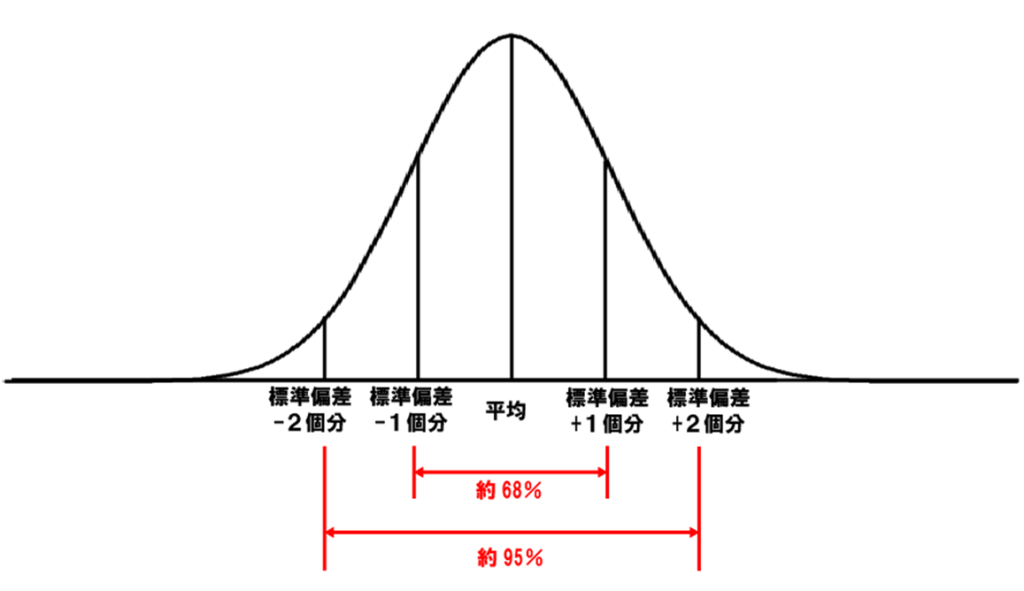
この散らばり具合はσ（シグマ）ともいい、集めたひとつひとつの結果が正規分布する集団でしたら、±１σ、±２σ、±３σを算出することで色々な考察が可能になってきます。
製造担当者さんの目線なら、

• 製造設備の完成度の評価
• （日毎・月毎の）製品出来高の評価
• ロットの歩留まり評価
• 工程改善をした場合のビフォー/アフターの比較　　

品質管理担当者の目線なら、

• 求めているレベルの品質で製品ができているか
• 狙い実際の品質項目値の差異評価
• トラブル発生の増減　

などが評価・考察できると思います。

「ちゃんと良いものができている!!」ということを表現するために、標準偏差で数値化することでより具体的に表すことができるのです。

「標準偏差」ではやれないこと。その弱点とは？

そうは言っても、工程分析をすのるに標準偏差さえ知っていれば完璧!!という訳ではありません。
たとえば、ある充填機Bで充填した重量が以下のとても小さな数字の場合、

1回目	0.00123kg
2回目	0.00104kg
3回目	0.00120kg
4回目	0.00108kg
5回目	0.00115kg

標準偏差値は次の値になります。

充填機Bでの標準偏差

0.0000796

この値だけを見て、何をどう評価できるでしょうか？わかりにくいと思いませんか？わかりにくい理由は、ゼロが多くて数値が果てしなく小さいことです。
この桁数ではでバラついてるのか何なのか、、、、逆に、とても小さな数字だから重量ばらつかない充填ができたのじゃない!?　と思ってしまうかもしれません。

で、もうひとつ。
Bよりやや大きめの充填機Cで充填した重量が次の数字の場合、

1回目	1.23g
2回目	1.04g
3回目	1.20g
4回目	1.08g
5回目	1.15g

標準偏差は次のようになります。

充填機Cでの標準偏差

0.0796

標準偏差の数値を見ると、充填機Bのほうが数字が小さく優秀！！のように見えますが、本当でしょうか。。。
BとCは桁数が違えど、1回目から5回目までの数値はまったく同じにしてあるので、感覚的にもわかるように、散らばり具合は同等なはずなんです。

散らばり具合･･･B=C

なのです。これが標準偏差だけを追っかけている場合に陥ってしまうことのある「弱点」なのです。

弱点を補う”とっても簡単”な手法とは？

この問題を解決するには
標準偏差が弱いところは、絶対評価でしかないところです。同じ場所を、同じ工程と整備で、同じ製品を同じロットサイズで連続的に作っているのなら、まぁこれだけで充分でしょう。

例えば充填機Bと充填機Cの比較でなくて、充填機Bだけでも、製品サイズが違ったり、ロット本数が違う場合は絶対評価である標準偏差では比べられないのです。

そういう、どちらが優れているかを比較する場合に使うべき統計的手法は「相対標準偏差」というものになります。

変動係数とも言いますがいずれも同じ意味です。

そして、何も難しい話では無く、計算式を覚えるのは簡単で、標準偏差を平均値で割るだけなんです。

変動係数=標準偏差/平均値（％）･･･D

相対標準偏差（変動係数）の威力を紹介

どうやって使う？
先ほどの充填機Bと充填機Cの例でお話しをしましょう。

うえのDの計算式を使って標準偏差と相対標準偏差をまとめました。

充填機B
標準偏差	0.0000796
平均(kg)	0.00114
相対標準偏差	6.99％

充填機C
標準偏差	0.0796
平均(g)	1.14
相対標準偏差	6.99％

さぁ、これでどちらが優れているか？の評価がわかりましたね。

6.99％のばらつきで両機にあり、同等であることが計算式から証明できました。

計算するのは何のため？　～結果からの改善への試み～

今回の評価からBとCの充填機は同じバラツキ精度で充填できることがわかりました。

さて、この結果から起こせるアクションは何しょうか？
工程と設備的には同等のレベルですが、そもそも充填量のサイズが違うことから充填ロス量が違います。充填機Cのほうが原料のロスが多く出ています。

そしてその後日。。。。

充填機Cの担当者がロスを減らす目標を立て、充填精度をさらに上げるための改善をしました。
改善後の結果の充填結果が次のようになりました。
製品の充填重量が１回目　1001.14g、２回目　1001.04g、３回目　1001.10g、４回目　1001.07g、５回目　1001.11g
Dの計算式を使うと、＝3.51％
今回の評価と改善を行ったことから、ロスを半減する改善につながりました（6.99％→3.51％へ）。

標準偏差の値を追っているだけでは、今回の改善にはつながりませんでした。
相対標準偏差を使いこなすことで、改善につながり、さらに、どの程度の改善ができたのか理論的に説明がでるのだと思います。

そこで終わっちゃダメ。　この次は改善アピールを！！

ロスを半減する改善!!　すばらしいことですが、この成果を上司にどのように報告したら自分の評価が上がるでしょうか！？それについては、別の記事でまとめています。

👇

報告書の書き方　-最善のアピール方法とは